Espiral inspirar
La espiral es una línea curva plana
cíclica que se inicia en un punto y rota alejándose del centro expandiéndose hasta el infinito. La espira se incrementa, pero vuelve a la misma posición desde una distancia diferente.
La espiral es una forma que se
identifica con facilidad en la naturaleza como en el crecimiento de las conchas de los gasterópodos.
Esta espiral puede ser de crecimiento equiangular o logarítmico. En los
seres vivos la espiral cumple una función práctica y es la de ocupar un espacio mínimo con una longitud máxima, es decir, envuelve.
La espiral en los seres vivos
aparece en: caracoles, caracolas, nautilus, cola
del caballito de mar, cola del camaleón, lengua de la mariposa, gusanos y
serpientes enroscadas, amnonites, garfios de las plantas trepadoras, girasoles,
margaritas, piñas, rosas, colas de mamíferos, trompas de elefantes, cuernos de herbívoros,
la doble hélice del ADN, el caracol del oído interno humano, yemas de los dedos o huellas dactilares, frondas de los helechos,…
La espiral en fenómenos naturales
la podemos ver en: olas de mar, remolinos del agua y
las nubes, tornados, huracanes, galaxias, turbulencias del aire, caída
rotatoria de cuerpos por efecto de la gravedad, las turbulencias de los
fluidos,...
El ser humano ha tomado como modelo la naturaleza y ha creado espirales para sus construcciones artificiales. La ha utilizado en la técnica, la arquitectura, el diseño, la artesanía, la decoración, y el arte, y a veces con un significado simbólico. Algunos de los ejemplos de espirales artificiales serían: capiteles jónicos, mosaicos romanos, laberintos, terminaciones de instrumentos musicales, desagües, el juego de la oca, setos de jardines y sus laberintos, diseños gráficos, tatuajes ta-moko maoríes, broches, pendientes, bobinas, ensaimadas…
La proyección de la espiral en la
tercera dimensión se llama hélice y sus aplicaciones prácticas las encontramos
en: escaleras, columnas torsadas, decoraciones de cúpulas, minaretes, torres, pasta
alimenticia, tapacubos de automóviles, rizos para el pelo, chimeneas,
decoración de herrería, tornillo de Arquímedes, roscas en tornillos y tuercas, sacacorchos,
hélices de barcos o ventiladores, muelles, amortiguadores, molinos de viento, virutas
de madera de un sacapuntas, surcos de un CD-ROM,...
Las observaciones que se hicieron en la
naturaleza llevaron a intuir que la espiral se relaciona con el principio de la
fuerza vital cósmica. Los ciclos del tiempo encadenados, como las fases de la luna y las estaciones del año ininterrumpidas, se relacionan con la energía que impulsa el Cosmos y su evolución cíclica. La forma rotatoria abierta que evoluciona continuamente, por similitud, se asoció la renovación permanente de la vida, el crecimiento, la progresión, la regeneración, la fertilidad y el renacimiento.
El célebre símbolo del Yin y el Yang participa de una rotación doble que simbolizan los dos principios opuestos vitales equilibrados en una totalidad. Como la de inspirar y espirar en una respiración.
Por lo tanto, fue una figura utiliza desde la prehistoria por estas derivaciones emblemáticas que connota.
El célebre símbolo del Yin y el Yang participa de una rotación doble que simbolizan los dos principios opuestos vitales equilibrados en una totalidad. Como la de inspirar y espirar en una respiración.
Por lo tanto, fue una figura utiliza desde la prehistoria por estas derivaciones emblemáticas que connota.
El estudio de las civilizaciones y la historia del arte nos brinda
innumerables ejemplos de espirales. Los trisqueles sagrados celtas, que dibujan
espirales triples, tiene alusiones a la rotación solar, la
trinidad (pasado, presente, futuro) y el equilibrio (cuerpo, mente, espíritu). La vinculación con el simbolismo de la renovación se puede interpretar que las espirales grabadas en tumbas megalíticas; puede atribuirse el viaje desde la vida a la muerte y quizás su retorno. Otros ejemplos de espirales son el caduceo con dos serpientes enroscadas, el uroboros, los capiteles clásicos, los laberintos de Creta, de la catedral de Chartres y Amiens, y el movimiento serpentiforme de algunas esculturas como las de Miguel Ángel, los dibujos de Escher,...
Espirales
y laberintos.
Espirales y laberintos.
Las espirales se han utilizado
para la creación de laberintos, y este como una metáfora de la introspección y el crecimiento
personal. Si el laberinto tiene un solo camino tiene un
significado de auto-conocimiento y búsqueda interior. El camino que lleva desde el exterior al centro es una forma de meditación, de encuentro con el propio ser, y metáfora del peregrinaje hacia el interior para llegar a un crecimiento y evolución de la conciencia.
En cambio, un laberinto con múltiples
camino tiene un sentido de confusión, de desorientar a la persona para que no
llegue al centro.
Construcciones
de espirales.
La
espiral de núcleo triangular
A continuación se describe la realización de espirales mediante dibujos explicativos. Se inicia la construcción de una
espiral de núcleo triangular equilátero y su evolución paso a paso.
Espiral en el mundo natural (caracol)
y espirales aplicadas en una (reja).
La espiral de núcleo cuadrangular
Se inicia la construcción de una espiral de núcleo cuadrado y su generación paso a paso.
Espiral de una caracola natural y aplicación de la teoría de la espiral a un tapacubos de un automóvil.
La espiral de núcleo hexagonal
Se inicia la construcción de una espiral de núcleo hexagonal y su proceso paso a paso.
Las formas de la naturaleza tienen una construcción geométrica y se han aplicado a la tecnología.
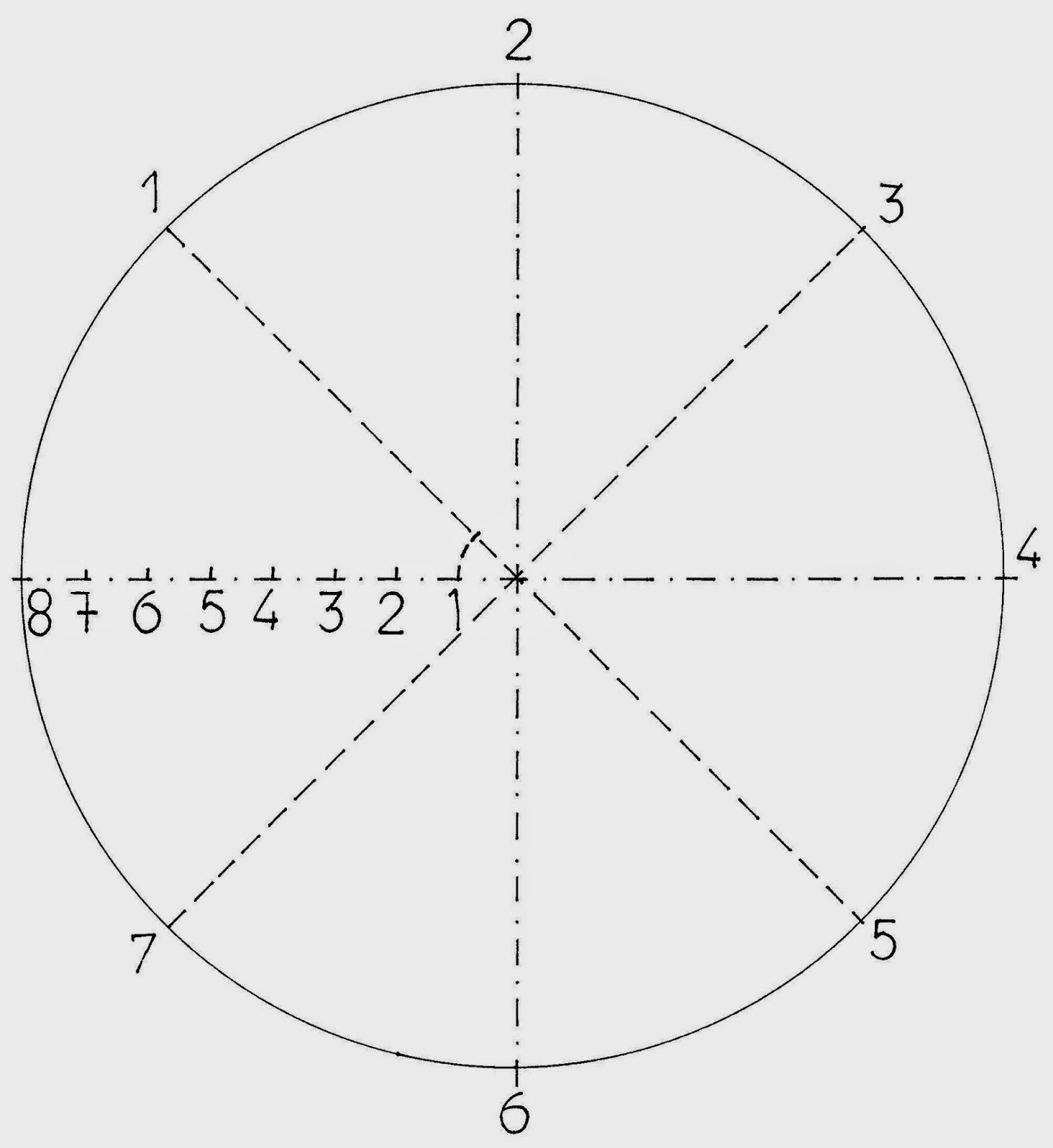
La espiral de núcleo circular
A partir de una circunferencia también es posible desarrollar una espiral, si tomamos como centro de giro su diámetro 1-2. Las distancias de giro parten del diámetro inicial y se van agrandando a medida que se gira 180 grados respecto a la horizontal. Es posible advertir que realizamos semicircunferencias de 180 grados; pero si dibujáramos las circunferencias completas serían tangentes entre sí.
La espiral de Arquímedes
Arquímedes de Siracusa diseñó una espiral que tenía aplicación para su famoso tornillo. Se muestra el proceso de construcción paso a paso.
Espiral de Arquímedes y la
homotècia.
La espiral de Arquímedes está relacionada con la homotecia. Los círculos concéntricos de la espiral los podemos observar en tres dimensiones como un cono que se expande. El vértice del cono es el centro de homotecia y la espiral es una consecuencia de su deslizamiento por la superficie del cono rotando.
Las distancias son proporcionales a los ángulos girados, d = K · A
Proporción constante del ángulo y el radio.
Ángulo/ Radio distancia,
45/1 = 90/2
= 135/3 = 180/4 = 225/5 = 270/6 = 315/7 = 360/8 = 45º = K, (constante)
La espiral jónica
La espiral jónica se utilizó en el capitel jónico.
Se muestran en estos dibujos el proceso para construir la voluta a partir de un cuadrado y cuatro centros.
Volutas en los capiteles clásicos
Orden jónico.
Los romanos tomaron las volutas del orden jónico y las hojas de acanto del orden corintio, la composición mezclada dio como resultado el orden compuesto.
La espiral de la sección áurea
La proporción áurea o divina proporción que se puede descubrir en el crecimiento de los seres vivos, genera una espiral, llamada la espiral de la sección áurea.

Números en la Naturaleza
Pitágoras expresó que todo lo que podemos encontrar en el Universo es armonía y número. Observando las piñas de los pinos y contando sus espiras se observa que en un sentido suele aparecer un número constante, y en el otro sentido otro número repetitivo. Estos dos números 8 y 13, al dividirse dan el célebre número de áureo
0, 618… ∞ ; o su inverso 0,618... ∞. Un número y una proporción que predomina en la naturaleza.
Se muestra en los siguientes dibujos como puede construirse a partir de un papel milimetrado. Se ha tomado como punto de referencia la conocida progresión de Leonardo Fibonacci y se ha trasladado a cuadrados que rotan a partir del origen 1·1
La circunferencia, la espiral y al hélice están unidas.
La hélice esférica

Números en la Naturaleza
Pitágoras expresó que todo lo que podemos encontrar en el Universo es armonía y número. Observando las piñas de los pinos y contando sus espiras se observa que en un sentido suele aparecer un número constante, y en el otro sentido otro número repetitivo. Estos dos números 8 y 13, al dividirse dan el célebre número de áureo
0, 618… ∞ ; o su inverso 0,618... ∞. Un número y una proporción que predomina en la naturaleza.
Sucesión de Fibonacci
La succesión de Leonardo
de Pisa, llamado Fibonacci, o sucesión de Fibonacci es una conocida sucesión que se puede descubrir en la naturaleza, es la siguiente:
1, 1, 2, 3, 5, 8,
13, 21, 34, 55, 89, 144, 233, 377, 610, ...
Número Áureo
Número Áureo
Al dividir cifras de la sucesión de Fibonacci estos se van aproximando cada vez más al número áureo.
Ф = 8/ 13
Ф = 8/ 13
Ф = 21 / 34
Ф = 34 / 55
Ф = 34 / 55
El número áureo es igual a: 0, 618,… Ф Phi (fi)
Φ = 0,161803 39887 49894 84820 45868 34365 63811 77203 09179 80576,... ∞
Φ = 0,61803 39887 49894 84820 45868 34365 63811 77203 09179 80576,... ∞
Números llenos de vida.
Este número irracional es conocido porque aparece en las piñas, los girasoles y en la proporción de las partes de muchos seres vivos; por ello se le llamó el número áureo, número de oro, número divino, proporción áurea, razón áurea,... Conocido desde la antigüedad se le considero el número que prefiere la naturaleza. Por su relación con el Cosmos y sus propiedades estéticas se cree que fue utilizado en obras de todas las artes. Se le asoció a la letra griega Ф Phi (fi), como homenaje al escultor griego Fídias el artífice del Partenón de Atenas, por la relación de esta obra con el famoso número.
Números llenos de vida.
Este número irracional es conocido porque aparece en las piñas, los girasoles y en la proporción de las partes de muchos seres vivos; por ello se le llamó el número áureo, número de oro, número divino, proporción áurea, razón áurea,... Conocido desde la antigüedad se le considero el número que prefiere la naturaleza. Por su relación con el Cosmos y sus propiedades estéticas se cree que fue utilizado en obras de todas las artes. Se le asoció a la letra griega Ф Phi (fi), como homenaje al escultor griego Fídias el artífice del Partenón de Atenas, por la relación de esta obra con el famoso número.
Al contar las espiras de los flósculos del girasol en sus dos sentidos de giro, estas se aproximan al número áureo.
El ser humano ha recogido las enseñanzas de la naturaleza y las ha aplicado con sabiduría, como vemos en este mosaico romano.
Las espiras de un cactus se corresponden con la sucesión de Leonardo Fibonacci. Las relaciones numéricas que construyen una espiral áurea las podemos encontrar en la naturaleza, son números llenos de vida.
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, ...∞
Una de las características de la espiral de la sección áurea es que crece al mismo tiempo en progresión aritmética y geométrica, veamos esta característica.
Progresión Aritmética
El ángulo de giro
crece en progresión aritmética,
sumamos de 90 grados en 90 grados:
0º, 90º, 180º,
270º, 360º, 440º, 530º, 620º,... ∞
Progresión Geométrica
El radio de giro crece en progresión geométrica.
Se multiplica por 0, 618,...
Crece de forma exponencial respecto al ángulo de giro
La espiral áurea
Se muestra en los siguientes dibujos como puede construirse a partir de un papel milimetrado. Se ha tomado como punto de referencia la conocida progresión de Leonardo Fibonacci y se ha trasladado a cuadrados que rotan a partir del origen 1·1
Progresión geométrica: en este dibujo se observa como los segmentos van creciendo de forma exponencial, se multiplica por el número de oro 0,618,.... ∞
Espirales
logarítmicas
Espiral logarítmica
Las espirales logarítmicas tienen un crecimiento geométrico y aritmético al unísono.
El ángulo crece en progresión aritmética, sumando siempre la misma cantidad. El radio de giro crece en progresión geométrica, multiplicando el radio anterior por el mismo número.
Ángulo crece en progresión aritmética:
0º, 30º, 60º, 90º, 120º, 150º, 180º, 210º, 240º, 270º, 300º, 330º, 360º
Sumamos cada vez 30 º
Radio de giro en crecimiento geométrico:
Radios: 4,1, 4,8 5,6 6,5 7,6 8,8 10,2 11,8 13, 9
Aproximadamente multiplicamos por por 1,6 , más o menos 1,175 cada vez.
La espiral de Richard Padovan
Espiral del número plástico o de Richard Padovan
La sucesión de
Richard Padovan o número plástico permite dibuja una espiral con una sucesión de cifras.
Successió de R.
Padavan: 1,2,3,4,5,7,9,12,21,28,37,49,65,86,….
El número plástico es : 1,324718,…
La espiral de rectángulos irracionales
Disponiendo los rectángulos irracionales de forma rotatoria puede diseñarse esta espiral:
Ángulo áureo
El ángulo áureo de los vegetales.
El ángulo áureo se da en los
vegetales y su rotación dibuja bellas espirales. Los pétalos, ramas u hojas de
las plantas crecen de forma que cada uno esté separado por un ángulo que
permiten que capten la luz solar y se distribuyan en el espacio de forma óptima.
Las hojas crecen rotando alrededor del tallo sin solaparse unas con otras de
forma que todas pueden recibir la luz. La medición del ángulo de giro se
realiza entre la base de una hoja y la siguiente, vista en la dirección del
eje. Siempre existe una hoja que está en la vertical de otra vista desde
arriba.
El ángulo áureo es el que divide
una circunferencia de 360 grados en proporción áurea y ese ángulo es: 137 º 30’ . Este ángulo permite que
las hojas al rotar nunca vuelvan estar en la misma posición, todas quedan
separadas y visibles para la fiesta solar.
Se obtiene de la siguiente forma:
Número de vueltas entre dos hojas
que están una sobre la vertical de la otra / Número de hojas en esta porción de
hélice.
Nº de vueltas / Nº de hojas =
1/1 ½ 1/3
2/5 3/8 5/13
8/21 13/34
El
ángulo áureo
Ángulo que parte el círculo en la
sección áurea es igual a 137º 30 ´
360º
- 137º 30´ = 222º 7´
360º/ 222º
7´ = 1, 6,… Ф Phi (fi)
222º 7´ / 360º = 0, 618,… Ф Phi (fi)
222º 7´ / 137º 30´ = 1, 6,…
Ф Phi
(fi)
Hélices
Hélice la espiral autorrealizadaLa circunferencia, la espiral y al hélice están unidas.
Las espirales planas bidimensionales se convierten en hélices cuando se
pasan al mundo tridimensional. Aplicando las transformaciones homográficas a la circunferencia, esta se puede mudar en cilindro, cono y esfera. El circulo puede tener un movimiento de traslación y se transforma en un cilindro. Si se produce una homotecia la circunferencia se transforma en un cono. Si el círculo se expande hasta un límite y posteriormente tiene una contracción idéntica se transforma en una esfera. Sobre estas formas geométricas (cilindro, cono y esfera) se pueden tomar puntos y dibujar sobre ellas hélices cuando las vemos en tres dimensiones y espiral se las proyectamos en dos dimensiones.
A continuación estudiaremos las hélices:
Hélice cilíndrica.
Hélice cónica.
Hélice esférica.
Hélice cilíndrica
El cilindro tiene un
vértice impropio en el infinito. La hélice arrollada sobre su contorno, se
confunde en planta con el perímetro de la circunferencia. Correspondería al
tornillo de Arquímedes, el yo-yo, el torno, brocas, roscas de botellas, la
pinza de ropa, muelles,...
Un cilindro es una circunferencia con movimiento de traslación.
La hélice cilíndrica
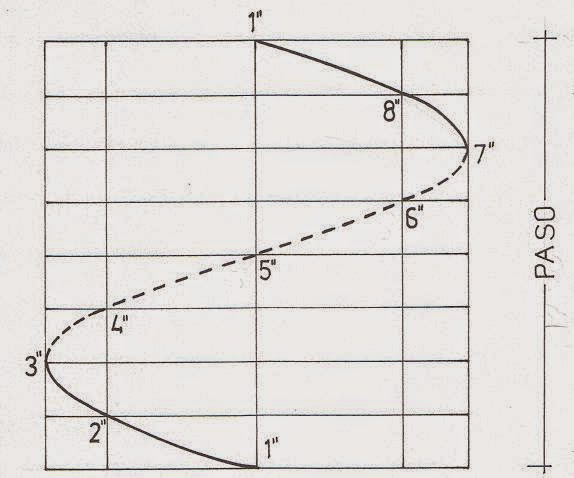
La hélice cilíndrica se obtiene tomando puntos constantes de la superficie de un cilindro.
Paso
El paso es el movimiento
alrededor del eje cuando se ha dado una vuelta completa respecto al eje.
Hélice cilíndrica y homotecia.
Al desarrollar el cilindro podemos observar como la hélice que estaba dibujada en su superficie es el Teorema de Tales, es decir una homotecia.
Hélice cónica
El cono tiene un
vértice propio. La hélice arrollada en su superficie, se ve en planta como una
espiral plana y correspondería al dibujo de la espiral de Arquímedes. Un ejemplo de esta espiral es el cono de la cabeza de un tornillo.
La hélice cónica
La hélice cónica se dibuja disponiendo puntos constantes sobre la superficie de un cono
Las cúpulas con forma de bulbosa y con rotación espiral son una aplicación práctica de esta forma.
La cúpulas con forma de bulbo y con una espiral rotatoria son propias de las iglesias ortodoxas.
Otras aplicaciones de la hélice cónica son: las carpas, cucuruchos, cúpulas, escaleras como las de la Sagrada Familia dentro de las torres, las hélices de aviones y barcos,...
Máquina voladora de Leonardo da Vinci.
Hélice
esférica
La esfera tiene un polo propio y las circunferencias se van
expandiendo hasta el ecuador con una curvatura positiva. En el alzado del dibujo anterior de la esfera, se ha
rectificado un cuadrante y después se ha referido a la esfera cada división.
Vista la circunferencia en planta vemos que los paralelos tienen una separación
progresiva. La hélice esférica en planta se ve como una espiral logarítmica,
equiángular o geométrica, y la curva descrita es una loxodrómica.
Loxodrómica.
La loxodrómica es una línea que une dos puntos cualesquiera de la superficie
terrestre, cortando a los meridianos con el mismo ángulo.
La loxodrómica era el rumbo de los navegantes de los siglos XVI y XVII; mantenían
el rumbo óptimo atravesando todos los meridianos con un ángulo constante. Sobre
la esfera tridimensional terrestre es la loxodrómica; pero sobre el plano es una espiral
logarítmica.
Angulo: 0º, 45º, 90º, 135º, 180º, 225º, 270º, 315º,
360º
Radios: 1 2,1
3,1 4,1 4,9
5,5 5,9 6
La proyección de la
loxodrómica esférica sobre un plano se convierte en una espiral equiángular o
logarítmica
La espiral inspira música
La circunferencia es obsesiva,
La espiral tiene conciencia
y la hélice es un espiral virtuosa realizada
La circunferencia que gira constantemente sobre sí misma padece una obsesión compulsión; pero cuando se rompe el vicio de la compulsión, la circunferencia se libera de su pensamiento circular y comienza la aventura de ser una espiral, es decir: crece y evoluciona. De la misma forma que un pensamiento obsesivo se rompe y la conciencia se expande, reflexionando sobre sí misma, observándose y pensando, pero acrecentando la distancia entre cada pensamiento. La espiral inspira música. Cuando la espiral es virtuosa y sueña, entonces se desarrolla plenamente y se transforma en una hélice. La hélice comienza a tocar la música compuesta por la espiral. La hélice es la música de la vida.
El circulo es vicioso, la espiral es consciente, la hélice sueña y se autorrealiza con plenitud. Visto desde un punto de vista metafórico: el círculo es un ritmo obsesivo, la espiral compone música, y la hélice es la sinfonía musical de la vida.
Mis mejores deseos



























































































































































No hay comentarios:
Publicar un comentario